El siguiente es enlace que los diseccionara a la pagina oficial del departamento de ciencias básicas de la Fundación Universitaria Los Libertadores, en donde encontraremos información del curso, así como contenidos, y guías programadas para el desarrollo del mismo.
martes, 29 de mayo de 2012
REGRESION Y CORRELACION LINEAL (LINK)
El siguiente enlace nos muestra una sencilla guia respecto al tema de REGRESION Y CORRELACION LINEAL.
REGRESIÓN
Si se dispone de dos series de datos emparejadas, con frecuencia se desea
conocer si ambas variables están relacionadas o si son independientes. Por
ejemplo, ¿en qué medida, un aumento de los gastos en publicidad hace aumentar las ventas de un determinado producto? ó ¿será que existe alguna relación entre la talla y el peso de una persona?
A continuación, representaremos la relación entre dos variables mediante una
gráfica llamada diagrama de dispersión, luego, estableceremos un modelo
matemático para estimar el valor de una variable basándonos en el valor de otra, en lo que llamaremos análisis de regresión y finalmente estudiaremos el grado de relación existente entre las variables en lo que llamaremos análisis de correlación.
La relación existente entre dos variables puede ser lineal, cuadrática, exponencial, logarítmica, etc.
DIAGRAMA DE DISPERSIÓN
En un plano cartesiano se representan tantos puntos como pares de observaciones se tengan, correspondiendo cada punto a un par de observaciones; a esta representación gráfica se le denomina indistintamente diagrama de dispersion.
RECTA DE REGRESIÓN
Se llama así a la recta que atraviesa la nube de puntos y que mejor se ajusta a ellos. El modelo matemático que describe una relación lineal cuando se estima el valor de Y en función de x esta dada así, Y = bx + c ó Y = 1x + 0, o Y = Bx + A. (Esta última notación es la empleada en las calculadoras CASIO)Donde:
Y es la variable que se va a estimar en función de otra variable (x) que se supone conocida. Se le denomina también como variable dependiente, explicada o predictando.
x es la variable cuyo valor supuestamente se conoce, se le denomina variable
independiente, predictor o explicativa.
b = 1 es la pendiente o sea la que determina el ángulo de inclinación de la recta.
Denominada coeficiente angular, cuantificando la cantidad que aumenta o decrece Y por cada unidad que aumente o disminuya la variable independiente x.
Si b es positivo indica que la recta es ascendente. Si b es negativo la recta será descendente y si b es igual a cero será una paralela al eje horizontal.
c = 0, corresponde al coeficiente de posición. Es el valor donde la recta
intercepta al eje Y. Puede ser mayor, menor o igual a 0.
Se debe encontrar la línea que represente al conjunto de puntos, para lograr esto se deben determinar los coeficientes de regresión muestrales (Coeficiente angular y de posición) que son estimadores de los parámetros o coeficientes de regresión poblacional. Los valores de b y c corresponden a aquellos que hacen que los Yi sean lo más cercanos posibles a los valores observados yi, para determinarlos lo más indicado es aplicar el método de los mínimos cuadrados.
CRITERIO DE LOS MÍNIMOS CUADRADOS:
En el método de los mínimos cuadrados se emplean los datos de la muestra para determinar los valores de b y c que minimizan la suma de los cuadrados de las desviaciones entre los valores observados de la variable dependiente yi, y los valores estimados de la variable dependiente, Yi. Este criterio se puede expresar así:
Mín ( yi – Yi)2
Siendo
yi = valor observado de la variable dependiente para la i-ésima observación.
Yi = valor estimado de la variable dependiente para la i-ésima observación.
GRÁFICAS ESTADÍSTICAS
Las gráficas estadísticas nos permite “familiarizarnos” con los datos que se han recopilado y resumido. Se considera como una técnica inicial de ANÁLISIS
EXPLORATORIO DE DATOS que produce una representación visual. Las graficas resultantes revelan un patrón de comportamiento de la variable en estudio. Se ofrecen muchos tipos de gráficos para describir el conjunto de datos. Dependiendo del tipo de datos y lo que se quiera representar, se hará uso del método gráfico más adecuado.
ELEMENTOS DE UNA GRAFICA:
En general se deben tener en cuenta los siguientes elementos:
1.Titulo
2.Tabla o Distribución de Frecuencias
3.Escala
4.Cuerpo de la gráfica
5.Convenciones
6.Notas aclaratorias
7.Numeración.
DATOS CATEGÓRICOS
DIAGRAMA CIRCULAR
Es de especial utilidad para mostrar proporciones ( porcentajes ) relativas de una variable. Se crea marcando una porción del círculo correspondiente a cada categoría de la variable .
DIAGRAMA DE BARRAS
Es una forma gráfica de representar datos cualitativos que se han resumido en una distribución de frecuencias, de relativas o de porcentuales. Hay varios tipos de gráficos de barras, como son :
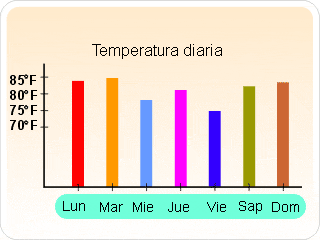
GRÁFICA SIMPLE DE BARRAS VERTICALES
Para respuestas categóricas cualitativas en el que solo interviene una barra para cada clase. Su trazo se realiza ubicando en el eje horizontal de la gráfica los nombres que identifican cada una de las clases. En el eje vertical se usa una escala de frecuencias, una de frecuencias relativas o una de porcentuales. Luego, con una barra de un ancho fijo trazada sobre cada indicador de clase llegamos a la altura que corresponde al tipo de frecuencia escogido. Las barras se separan a fin de señalar que cada clase es una categoría independiente. Los espacios entre las barras deben corresponder a la mitad del ancho de una barra.
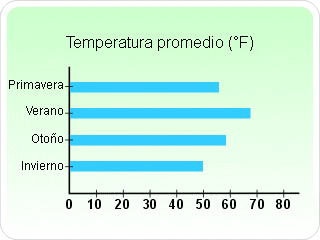
GRÁFICA SIMPLE DE BARRAS HORIZONTALES
Se utiliza principalmente para facilitar la comparación entre las diferentes clases que componen los datos categóricos. El trazo de la gráfica es muy similar a la gráfica de barras verticales, solo que éstas van en forma horizontal y están ordenadas de la mayor a la menor frecuencia absolutas, de frecuencia relativas o de porcentajes. De esta manera se logra una mejor visualización en las preferencias.
GRÁFICA DE BARRAS COMPONENTES
Este tipo de gráfica se usa cuando las diferentes categorías de datos se componen de otras clases , de tal forma que cada barra se pueda subdividir y representar cada una de estas clases .Así mismo, entre las categorías y sus componentes se compara valores.
También se le conoce como barras agrupadas. Se puede hacer uso de barras
horizontales o de barras verticales; su escogencia depende de lo que se pretenda ilustrar para que facilite su visualización.
GRÁFICA DE BARRAS SECCIONADAS
Esta gráfica compara entre categorías el aporte de cada valor al total ,dando lugar a una columna apilada para cada clase. También se puede presentar de manera horizontal o vertical
DIAGRAMA DE PARETO
Es un tipo especial de diagrama de barras verticales, donde las respuestas categóricas se grafican en orden descendente de frecuencias y se combinan con un polígono acumulado en la misma escala. El diagrama de Pareto se usa ampliamente en el control estadístico de procesos y el control estadístico de la calidad del producto.
Lo que se pretende con este tipo de grafico es describir en donde se presenta el mayor porcentaje del problema y que factores lo afectan. Este concepto, se conoce como la regla de 80-20, considera que el 80% de la actividad se debe al 20% de los factores . Al concentrarse en el 20% de los factores, los gerentes pueden atacar el 80% del problema.
DIAGRAMA DE BARRAS
Tienen el mismo uso que los datos categóricos, solamente que intervienen dos variables, una que representa el tiempo y la otra cantidad ( Ingresos, ventas, IPC, Costos, No. De unidades producidas, etc.). Dependiendo de lo que se quiera representar se ofrecen los diagramas de barras simples, de componentes, bidireccional y seccionadas.
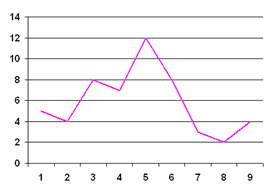
GRÁFICAS DE LINEA
Se ilustra mediante segmentos de línea los cambios en cantidades con respecto al tiempo. Son especialmente útiles en el comercio y en los negocios.
DATOS NUMERICOS
HISTOGRAMAS
Una de las maneras más comunes de representar una distribución de frecuencia . Su grafica consiste en un conjunto de barras, en la que la base de cada barra representa una clase o intervalo, indicada en el eje horizontal, y la altura por su frecuencia, indicada en el eje vertical. Generalmente las barras se trazan adyacentes una a la otra.
POLÍGONO DE FRECUENCIA
De segmentos de línea que conectan los puntos formados por la intersección del punto medio de clase y la frecuencia de clase absoluta, relativa o porcentual.
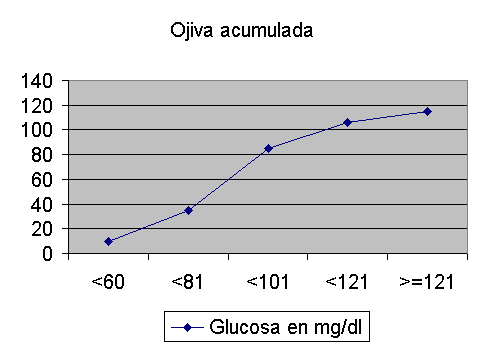
OJIVA
Es un polígono acumulado de frecuencia absoluta ,relativa o porcentual y por lo tanto representa segmentos de línea que se origina al conectar los puntos formados por la intersección entre el límite inferior de cada clase con la frecuencia acumulada. Es conocida como POLÍGONO DE FRECUENCIA ACUMULADA MENOR QUE , ya que muestra el número o porcentaje de observaciones menores a cierto valor. La ojiva es importante por que nos permite extrapolar información que la distribución de frecuencia oculta y así como calcular estadísticos como la mediana, cuartiles, deciles y percentiles, en forma aproximada. Para construir la ojiva se debe primero elaborar la distribución de frecuencia menor que.
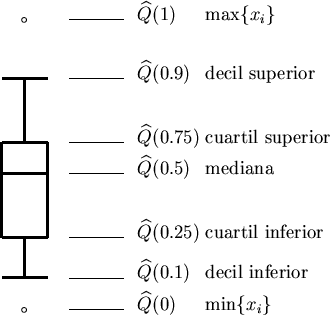
DIAGRAMA DE CAJA
Es una representación gráfica, basada en cinco números estadísticos: valor mínimo, Q1 , la mediana, Q3 y valor máximo. Se utiliza como una técnica de ANÁLISIS EXPLORATORIO DE DATOS y tiene la ventaja de que no se requiere de la desviación estándar, ni de la media aritmética y así como de resumir los datos en una distribución de frecuencia, situación que si necesita el histograma, el polígono y la ojiva. Para su trazo, se lleva a cabo
los siguientes pasos:
1. Crear una escala apropiada a lo largo del eje horizontal
2. Dibujar una caja entre el Q1 y el Q3
3. Dentro de la caja trazamos una línea recta vertical que representa la mediana
4. Finalmente, trazamos líneas horizontales de la caja hasta el valor mínimo y de la caja hasta el valor máximo. A estas líneas horizontales fuera de la caja se les conoce como “bigotes”
COMPONENTES DE UNA INVESTIGACIÓN ESTADÍSTICA
El estudio estadístico de una situación con propósitos inferenciales se centra en dos conceptos fundamentales: población y muestra, los cuales serán definidos a continuación:
Población. Es el conjunto formado por todos los valores posibles que puede asumir, la variable objeto de estudio.
Así por ejemplo, en un estudio sobre la preferencia de los votantes en una elección presidencial, la población consiste en todas las respuestas de los votantes registrados. Pero el término no sólo está asociado a la colección de seres humanos u organismos vivos; y tenemos así que, si se va a hacer una investigación de las ventas anuales de los supermercados, entonces las ventas anuales de todos los supermercados constituyen así mismo la población.
Es bueno tener en cuenta que el término población se interpreta de dos maneras cuando se hace un estudio estadístico, a saber:
1. La interpretación propia en el Análisis Estadístico, que corresponde a la que hemos presentado anteriormente.
2. Como el conjunto de objetos sobre los cuales actúa la variable considerada.
Por tanto, no es extraño escuchar expresiones tales como, "se hizo un estudio de los niveles de ingreso de la población trabajadora colombiana", entendiéndose con ello que el elemento estadístico objeto de análisis fue el registro numérico de los ingresos.
Muestra. Es cualquier subconjunto de la población, escogido al seguir ciertos criterios de selección.
La muestra es el elemento básico sobre el cual se fundamenta la posterior inferencia acerca de la población de donde se ha tomado. Por ello, su escogencia y selección debe hacerse siguiendo ciertos procedimientos que son ampliamente tratados en la parte de la estadística llamada Teoría de muestreo.
El concepto de muestra tiene también las dos connotaciones que hemos señalado para la población.
Las características de una población se resumen para su estudio generalmente irá mediante lo que se denominan parámetros; éstos a su vez se toman o consideran como valoresverdaderos de la característica estudiada. Por ejemplo, la proporción de todos los clientes que declaran cierta preferencia por una marca particular de un producto dado, es un parámetro de la población de todos los clientes; es la verdadera proporción de la población.
Igualmente, la media aritmética de las cuentas corrientes de los clientes de un banco determinado constituye un parámetro de la población de las cuentas de los clientes de ese banco.
Cuando la característica de la población estudiada se reduce a una muestra el resumen de esa característica se hace mediante una esta (medida) o estadígrafo. Así por ejemplo. si se toman 100 de todos los posibles clientes y se les entrevista para ver si están a favor de una marca particular de un producto, estos 100 clientes la constituyen una muestra.. Si hay 70 clientes que prefieren dicha marca entonces la proporción muestral será 0.70 y constituirá un estadígrafo; de igual manera si se escogen 1,000 cuentas del total de las cuentas comentes; las 1,000 observaciones conforman una muestra y el promedio aritmético de estas cuentas un estimador.
La inferencia estadística se orienta a sacar conclusiones acerca del parámetro o parámetros poblacionales con base en el valor de un estimador obtenido a partir de los datos muestrales extraídos de esa población. Para llegar a ese objetivo a través de un proceso racional y eficaz, se aconseja que se tengan en cuenta los siguientes pasos:
1. Formulación del problema. En este punto se debe especificar de manera clara la pregunta que se debe responder y la población de datos asociada a la pregunta. Los conceptos deben ser precisos y deben ponerse limitaciones adecuadas al problema motivadas por el tiempo, dinero disponible y la habilidad de los Investigadores.
Algunos conceptos como, artículo defectuoso, económico, salario, pueden variar en cada caso y para cada problema debemos coincidir con las ideas señaladas en el estudio.
2. Diseño del experimento. Este aspecto es de gran importancia, puesto que la recolección de datos requiere dinero y tiempo. Es siempre nuestro deseo obtener máxima Información con el mínimo costo (dinero y tiempo) posible. Incluir excesiva Información en la muestra es a menudo costoso y antieconómico. Incluir poca también es poco satisfactorio. Esto implica, entre otras cosas, que debemos determinar el tamaño de la muestra o la cantidad o tipo de datos que nos permita resolver el problema de la manera más eficiente.
3. Recolección de datos. Esta parte, por lo general, es la que exige más tiempo en la Investigación. Esta recolección debe ajustarse a reglas estrictas ya que de los datos esperamos extraer la Información deseada.
4. Tabulación y descripción de los resultados. En esta etapa, los datos muestrales se exponen de manera clara y se ilustran con representaciones tabulares y gráficas (diagramas. histogramas, etc.); además se calculan las medidas estadísticas apropiadas al proceso inferencial que haya sido escogido.
5. Inferencia estadística y conclusiones. Este último paso constituye tal vez la contribución más importante de la estadística al proceso inferencial. Aquí se fija el nivel de confiabilidad para la inferencia; esto es debido a que las conclusiones derivadas de inferencias estadísticas jamás se pueden tomar con un 100% de certeza, pero sí se les puede asociar un nivel de confiabilidad; en términos de probabilidad denominados nivel de confianza y nivel de significancia. El proceso Inferencial nos llevará a una conclusión estadística que servirá de orientación a quien o quienes deban tomar la decisión (administrativa o clínica) sobre el tema objeto de estudio.
VARIABLE Y TIPO DE VARIABLES
Con el propósito de no crear en el estudiante un estado de desaliento, resultado de la confusión propia cuando se empiezan a manejar conceptos abstractos, hemos preferido dejar de lado el excesivo formalismo, presentar las ideas de la manera más simple posible y procurando que queden lo más adecuadas al lenguaje Estadístico.
Variable. Es toda característica que toma diferentes valores en distintas personas, lugares o cosas. Por ejemplo, la estatura de las personas, el número de personas que residen en una vivienda, el sexo de los estudiantes de la universidad.
Datos. Son números o medidas que han sido recopilados como resultados de observaciones. Los datos pueden provenir de recuentos tales como el número de personas que laboran en una empresa o de mediciones como el peso de una persona.
Variable aleatoria. Cuando los valores que asume la variable han sido antecedidos por una selección aleatoria de los objetos medidos o son resultados de algún proceso al azar. A las variables aleatorias usualmente se les denota por letras X. Y, Z; y a los valores por las respectivas minúsculas.
Si de las cuentas corrientes de los clientes de un banco se escogen cinco al azar en un día determinado, la variable depósito en cuenta corriente de cada cliente constituye una variable aleatoria que podemos designar X. Si alguna de las cuentas aparece con un registro o saldo de 1.000.000 de pesos entonces x = 1.000.000.
Variable continua. Es aquella que teóricamente puede tomar cualquier valor dentro de un intervalo. Por ejemplo, la estatura de las personas o el tiempo necesario para realizar una transacción bancaria de parte del cliente.
Variable discreta. Es aquella que toma valores separados entre sí por alguna cantidad. Por ejemplo, el número de personas que llegan en una hora a un banco a solicitar un servicio.
Variable cuantitativa. Es aquella que asume valores acompañados de una unidad de medida. Por ejemplo, el número de accidentes anuales ocurridos en una carretera de mucha circulación o el ingreso por familia en determinados sectores de la ciudad.
Variable cualitativa. Es la que se refiere a clasificación, como estado civil, preferencia por una marca, etc.
FENÓMENOS QUE ABARCA Y NO ABARCA LA ESTADÍSTICA
Los fenómenos o hechos que continuamente suelen suceder presentan ciertas características tales como las de ser observados y manifestarse al exterior mediante registros, al mismo tiempo el de cuantificarse y aun el de poder determinar la intensidad con que se produce cierto fenómeno.
El campo de acción de la Estadística es muy amplio, sin embargo, no todos los fenómenos son abarcados. Únicamente aquellos que reúnen ciertas condiciones a saber:
1. Fenómenos colectivos o de grupos.
2. Fenómenos de frecuente repetición.
3. Fenómenos de distinta frecuencia.
4. Fenómenos distantes en el espacio.
5. Fenómenos distantes en el tiempo.
6. Fenómenos cualitativos que puedan cuantificarse.
En cambio quedan fuera del campo de acción de la Estadística, los enumerados a continuación.
1. Fenómenos individuales.
2. Fenómenos que no se exteriorizan.
3. Fenómenos accidentales en el tiempo y en el espacio.
4. Fenómenos cualitativos que no puedan cuantificarse.
GENERALIDADES
En la vida diaria los diversos fenómenos de orden económico, social, político, educacional, e incluso biológico, aparecen, se transforman, y finalmente desaparecen. Para tan abundante y complejo material es preciso tener un registro ordenado y continuo de conseguir en un momento dado los datos necesarios para un estudio de lo que ha sucedido, sucede o puede suceder.
Para ello es necesario contar con un método, con un conjunto de reglas o principios, que permitan la observación, el ordenamiento, la cuantificación y el análisis de dichos fenómenos. Ese método es el que se denomina ESTADÍSTICA.
La palabra ESTADÍSTICA se refiere a un sistema o método científico usado en la recolección, organización, análisis, interpretación numérica de la información. También se puede decir que la ESTADÍSTICA estudia el comportamiento de los fenómenos de grupo. Hay dos fases en el campo de la Estadística. En primer lugar, está la fase que solo se limita a la descripción y análisis de una serie de datos sin llegar a conclusiones o generalizar con resultados a un grupo mayor. Esta (fase) se conoce como Estadística deductiva o descriptiva. En segundo lugar esta la fase que trata de llegar a conclusiones acerca de un grupo mayor basada en información de un grupo menor o muestra: es esta la estadística inductiva o inferencial. Las conclusiones a que se llega respecto a la población o universo, se exponen en términos probabilísticos, sin estar completamente seguros de estas inferencias.
Desde el punto de vista descriptivo analítico, la Estadística se define como un conjunto sistemático de procedimientos para observar y describir numéricamente los fenómenos, descubrir las leyes que regulan la aparición, transformación y desaparición de los mismos.
Generalmente se asocia la palabra ESTADISTICA con cifras sobre algún campo particular. Podemos asociarla sobre el número de nacimientos, defunciones, transacciones comerciales, valor de las acciones en el mercado de valores, el volumen físico y monetario o importaciones, el beneficio y utilidad de las empresas o la demanda presente o potenciar algún producto. Cuando usamos la palabra Estadística es para referirnos más bien a datos tabulados y ordenadamente presentados.
HISTORIA
ESTADÍSTICA
La estadística es un conjunto de teorías y métodos que han sido
desarrollados para tratar la recolección, el análisis y la descripción
de datos muestrales con el fin de extraer conclusiones útiles,
Su función primordial es apoyar al investigador al decidir
sobre el parámetro de la población de que procede la muestra.
UNCOLN L. CHAO.
El estudio de la Estadística ha sufrido cambios sustanciales desde sus comienzos. Merecen mención especial dos fuentes de tendencias de desarrollo. Primeramente, el origen de la Estadística puede advertirse ya en la necesidad de datos numéricos en los estados que surgían de la sociedad medieval en la Europa Occidental. Al transformarse la sociedad medieval en el estado político, el nuevo gobierno necesitaba información sobre los recursos
del país para poder tener éxito. Así pues era obligado para los nuevos gobernantes el obtener descripciones numéricas, tales como el número de ciudadanos de las diversas unidades políticas bajo su jurisdicción: ciudades, condados y provincias. El término Estadística, que se deriva del latín status, que significa estado en el sentido político, se empleo entonces para referirse a la recolección y descripción de tales datos del estado. La necesidad de acopiar y analizar datos numéricos impulsó a desarrollar métodos para
facilitar la labor, que era lo que constituía lo más considerable de la Estadística hasta la era moderna.
No es necesario enumerar todos los que contribuyeron al desarrollo de los métodos estadísticos. Pero se ha de mencionar sin embargo al belga Adolph Quetelet (1796 - 1874), que fue el primero en aplicar métodos modernos a conjuntos de datos. Suele llamarse a Quetelet "padre de la Estadística moderna" por su continua insistencia en la importancia de aplicar métodos estadísticos. Sus distinguidas contribuciones a la práctica y a la metodología estadísticas cubrieron muchos campos de la estadística oficial, tales como los
censos, el desarrollo de la uniformidad y comparabilidad de estadísticas entre las naciones, y la organización de la primera conferencia Estadística internacional, La Comisión Central de Estadística, que Quetelet fundó, fue el modelo para instituciones similares en otros países.
Otra fuente de la Estadística se encuentra en la atención prestada al juego en el siglo XVII. Debido a la tolerancia y al prestigio de que disfrutaban varias formas de juegos para recreación de la nobleza de Inglaterra y Francia durante este período, se suscitó un interés intenso por los juegos de azar, cosa que sin proponérselo, llevó al desarrollo de la teoría de las Probabilidades. Y entre tanto, existía ya una tecnología lo bastante avanzada como para suministrar dispositivos para juegos, tales como dados y cartas, con suficiente refinamiento como para desafiar la aguda imaginación del matemático. El jugador depende del azar o posibilidad de error asociada a una línea de acción dada; el resultado efectivo de una prueba es cosa desconocida, pero la teoría de las Probabilidades da el número esperado de
ocurrencia de un suceso particular en un número muy elevado de pruebas. La Estadística moderna se interesa enormemente por dicha teoría.
Al mismo tiempo, los estudios de Probabilidades requerían el tratamiento matemático de los errores en las mediciones, de lo que resultaron teorías y métodos desarrollados para describir las configuraciones de distribución de tales errores. Ya desde el siglo XVIII se había observado que las medidas repetidas de un cierto objeto o fenómeno daban lugar a una configuración en la distribución de los errores que tenía la forma de una curva acampanada. La curva es simétrica con respecto al valor verdadero, lo cual significa valor
de error nulo, que queda en el centro. Es simétrica porque las desviaciones negativas y positivas respecto del centro son iguales en magnitud y frecuencia. Cuanto mayores las derivaciones menores serán las frecuencias.
A propósito de la evaluación de los errores de observación en astronomía, se hizo un descubrimiento de importancia mayor para la estadística. La distribución de errores resultante con su forma de campana Y su simetría se llama curva normal de errores. También se dice distribución gaussiana de errores, por el nombre de su descubridor Karl Frierich Gauss (1777 - 1855).
Entre los contemporáneos de Quetelet y Gauss que contribuyeron al avance de la estadística como ciencia estaban Florence Nightingale (1820 - 1910) Y Francis Galton (1822 - 1911).
Florence Nightingale creía firmemente en los métodos Estadísticos. Sostenía que todo director debería guiarse por el conocimiento estadístico si quería tener éxito y que los políticos y los legisladores fracasaban frecuentemente por la insuficiencia de sus conocimientos estadísticos. Galton, como su primo Charles Darwin, se interesó profundamente en el estudio de la herencia, a la cual aplicó métodos estadísticos. Entre sus principales contribuciones se encuentra el haber desarrollado métodos tan fundamentales como la regresión y la correlación.
La obra de Galton fue estímulo para una serie de investigaciones de Karl Pearson (1857 - 1936), el cual inició la publicación del periódico Bíométrica, que ha influido profundamente en el desarrollo de la estadística. Muchos de los métodos Estadísticos fueron descubiertos por Pearson, siendo el más importante la distribución ji - cuadrado, que encontró en 1990.
En el siglo XX, quienes han contribuido de manera más descollante al estudio de la estadística han sido William S. Gosset (1876 - 1937) Y Sir Ronald Fisher (1890 - 1962). Gosset, que escribía bajo el seudónimo "Student", dedujo la distribución t y su contribución especial fue en el campo de la teoría de pequeñas muestras. Fisher halló conocida distribución F y aportó contribuciones continuamente hasta 1962, muchas de ellas han tenido grande influencia en los modernos procedimientos Estadísticos. Si bien su trabajo era sobre todo en los campos de la biología, genética y agricultura, su impacto ha llegado a todas las aplicaciones de la Estadística.
JUSTIFICACIÓN
El curso de Estadística I pretende desarrollar en los estudiantes las competencias propias al área, para poder realizar un análisis de estadígrafos básicos como la media, la varianza y la desviación estándar a partir de un conjunto de datos dado, al igual podrá describir probabilísticamente una distribución de datos, identificando el tipo de variable (discreta o continua) y por consiguiente el tipo de distribución de probabilidad.
Suscribirse a:
Comentarios (Atom)